Stress
Stress can be thought of the internal reaction to forces on an object.
This is one of the most important concepts in mechanics of materials, because materials fail as a result of high stresses. When a force is applied to an object that is unable to move (constrained in FEA terms) it must react those forces by deforming.
Stress can generally be broken down into 3 types: tensile (pulling) stress, compressive (squeezing) stress, and shear (sliding) stress. Tensile and compressive stress are often grouped and called normal stresses, as they acted perpendicular, or “normal to” a surface. Stress is denoted by the Greek lower case letter sigma (σ). Stress is calculated the same way as pressure, where σ=F/A.
These kinds of stress can be combined mathematically into a single form known as Von Mises stress. If the Von Mises stress exceeds the yield point anywhere in the part then we can expect the material to yield at that location. As the Von Mises yield criterion is the most empirically accurate way to judge yielding for ductile materials it is the standard form used in analyzing part stresses.
Strain and Deformation
Strain is the measure of the deformation (aka displacement) of a material. For an object being pulled in only one direction this equation is given simply as ϵ=ΔL\L. That is, strain is the change in length of the material divided by the original length of the material. It is often given as a decimal. Strain can also be measured as normal strain, or shear strain. These two kinds of strain together can be used to fully define the deformation of an object. The deformation of an object is often a major requirement in engineering applications, for example when two parts must not come into contact under load or when an object must be stiff to retain a particular geometry.
Stress-Strain Curves
Stress-strain curves are in many ways the key to understanding and applying the results of simulation analyses. Stress-strain curves are unique for each material, but many kinds of materials exhibit the same patterns of behavior as loads are increased.
Here we can see a stress-strain curve typical of a common ductile material such as mild steel under tensile loading. At the left side of the graph is the region where the material’s response is known as “linear-elastic.” Under elastic deformation the material will deform, but as the load is removed it will return to its original shape. This can be seen if you lightly flex a long metal rod, which will bounce back when you stop applying force.
How much the material will deform in the linear elastic range is measured by Young’s Modulus, which is measured as stress over strain.
Next, if more force is applied, the material will reach its yield strength. This is known as the yield point, and after this the material will experience “plastic deformation” or permanent deformation. Note that some materials, such as aluminum, have different stress-strain curves in which there is no clear “hump” at the yield strength, and so that number is calculated using a standard equation for when the material is said to have moved into the plastic deformation region.
Often, engineering applications want to avoid any permanent deformation, so the yield stress is used as the limiting stress in simulations. However, in certain specialized applications, such as crumple zones in a car, a product may be designed to yield in specific situations. The the amount of energy absorbed by a material is given by the area under the stress-strain curve. These advanced applications are beyond the scope of this explanation. We will also forgo explanations of strain hardening and necking, although these can be found online.
Brittle materials, such as cast iron and glass, exhibit very different stress-strain curves than ductile materials. These materials will fracture before undergoing any appreciable plastic deformation. This can be a very negative behavior in many situations, as these materials will likely not give obvious visual or audible indication before catastrophic failure. Their ultimate tensile strength may also vary widely based on even small variations in manufacture or structure.
Note the increased amount of energy absorbed by ductile materials of similar nature.
Various Limits and Strengths related to stress-strain curve
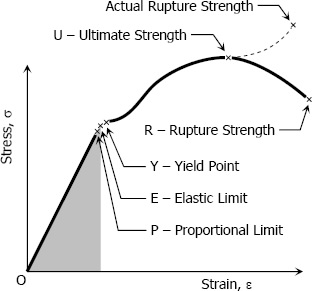
Proportional Limit (Hooke’s Law):
From the origin O to the point called proportional limit, the stress-strain curve is a straight line. This linear relation between elongation and the axial force causing was first noticed by Sir Robert Hooke in 1678 and is called Hooke’s Law that within the proportional limit, the stress is directly proportional to strain or
σ=kε
The constant of proportionality k is called the Modulus of Elasticity E or Young’s Modulus and is equal to the slope of the stress-strain diagram from O to P. Then
σ=Eε
Elastic Limit:
The elastic limit is the limit beyond which the material will no longer go back to its original shape when the load is removed, or it is the maximum stress that may e developed such that there is no permanent or residual deformation when the load is entirely removed.
Elastic and Plastic Ranges:
The region in stress-strain diagram from O to P is called the elastic range. The region from P to R is called the plastic range.
Yield Point:
Yield point is the point at which the material will have an appreciable elongation or yielding without any increase in load.
Ultimate Strength:
The maximum ordinate in the stress-strain diagram is the ultimate strength or tensile strength.
Rapture Strength:
Rapture strength is the strength of the material at rupture. This is also known as the breaking strength.
Modulus of Resilience:
Modulus of resilience is the work done on a unit volume of material as the force is gradually increased from O to P, in N·m/m3. This may be calculated as the area under the stress-strain curve from the origin O to up to the elastic limit E (the shaded area in the figure). The resilience of the material is its ability to absorb energy without creating a permanent distortion.
Modulus of Toughness:
Modulus of toughness is the work done on a unit volume of material as the force is gradually increased from O to R, in N·m/m3. This may be calculated as the area under the entire stress-strain curve (from O to R). The toughness of a material is its ability to absorb energy without causing it to break.
Working Stress, Allowable Stress, and Factor of Safety:
Working stress is defined as the actual stress of a material under a given loading. The maximum safe stress that a material can carry is termed as the allowable stress. The allowable stress should be limited to values not exceeding the proportional limit. However, since proportional limit is difficult to determine accurately, the allowable tress is taken as either the yield point or ultimate strength divided by a factor of safety. The ratio of this strength (ultimate or yield strength) to allowable strength is called the factor of safety.