Researchers at NASA’s Armstrong Flight Research Center have developed and tested a strain gage that surpasses conventional foil technology, which is limited to 20 percent strains. This was a significant shortcoming given that new structural components on aerospace vehicles include highly elastic, low Young’s modulus materials. For example, Kevlar®-reinforced rubber and elastomer have a non-linear stress-strain relationship with extreme rupture strains—some greater than 500 percent. Results from sensor tests indicate potential to use this new gage for elastic strain greater than 100 percent, with minimal localized stiffening. These tests indicate that, when used with specifically designed constant current signal conditioning, accurate static strain measurements are achievable for ground testing. Also, a conceptual temperature-compensation method has been conceived to greatly reduce measurement error for atmospheric flight applications in environments of –30 °F.
Benefits
- Robust: Provides high strain measurements—greater than 100 percent—with minimal localized stiffening of test articles
- Accurate: Offers a real-time temperature-cancellation method to minimize the effects of varying thermal conditions in aerospace applications, and provides constant current signal conditioning to eliminate post-test leadwire resistance corrections
- Proven: Is based on legacy medical-grade technology, with sensor tests at Armstrong to verify strain-measurement results; more testing on new substrates is planned
- Streamlined: Includes a data acquisition system that eliminates the need for two-point tensile calibrations
Applications
Myriad aerospace components and aircraft could benefit from the technology, including:
- Elastomer skins for highly flexed wing and control surfaces
- Rubberised fabric skin
- Cargo-carrying airships
- Inflatable wing-morphing aircraft
- Aeroservoelastic control
- High-cycle, high-strain fatigue testing
- Flexible wind turbine blades
Technology Details
Armstrong’s new strain gage technology was developed to meet the needs of various NASA projects. For example, the Adaptive Compliant Trailing Edge (ACTE) and Hypersonic Inflatable Aerodynamic Decelerator (HIAD) projects needed either high-elastic strain measurements of up to 180 percent or a low-modulus strain sensor that does not stiffen the rubberised fabric of test articles. Due to time constraints, fabricating a sensor from scratch was infeasible, so a similar gage used by the medical field was modified, prototyped, and tested to meet aerospace requirements.
How It Works
The original medical sensor that Armstrong’s technology is based on is a plethysmography sensor (measuring endothelial dysfunction) and wraps around a limb or finger to measure vascular flow. The sensor is primarily constructed of an indium-gallium liquid metal (LM)-filled, small-diameter silicone tube with electrical lead wires attached. When the LM is excited, length changes can then be determined by typical strain resistance changes over the initial resistance.
This original sensor was modified to lay flat and be attached to a test substrate in a single looped strain gage configuration. A simple tool was developed to reduce initial resistance scatter between gages and provide consistency in end-loop radii for conformity of transverse sensitivity. A new circuit design incorporated the excitation current required for a range of 1 million microstrain (i.e., 100 percent strain), with a step resolution of less than 10 micro strain, and was designed to compensate for changing temperatures in varying thermal environments. Taking advantage of constant current makes it possible to derive strain using accurate initial resistance measurements (Kelvin) and plugging them into the strain equation. A data acquisition system processes strain equations and eliminates the need for two-point tensile calibrations. Armstrong’s sensors were laboratory tested under both bending and single-axial tensile modes against conventional foil strain gages. Aluminium, Plexiglas®, and fiberglass materials were used for bending, and tensile testing was conducted on graphite-epoxy tensile coupons to 10,000 microstrain. Further testing used photogrammetry technology for higher strains on elastomer (greater than 100 percent) with excellent repeatability and accuracy.
Why It Is Better
Physical modifications to the original sensor make it more conducive to aerospace strain measurements. In particular, the streamlined profile of the sensor and single-loop strain gage grid shape give it a reasonably small footprint, minimal transverse sensitivity, and high elastic static strain measurements for ground tests. In addition, its real-time temperature-compensation method provides cancellation of thermal effects on the measurements while minimizing sensor footprint size for some flight applications.

 : momentum diffusivity (kinematic viscosity),
: momentum diffusivity (kinematic viscosity), 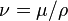 , (SI units: m2/s)
, (SI units: m2/s) : thermal diffusivity,
: thermal diffusivity, 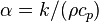 , (SI units: m2/s)
, (SI units: m2/s) : dynamic viscosity, (SI units: Pa s = N s/m2)
: dynamic viscosity, (SI units: Pa s = N s/m2) : thermal conductivity, (SI units: W/m-K)
: thermal conductivity, (SI units: W/m-K)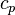 : specific heat, (SI units: J/kg-K)
: specific heat, (SI units: J/kg-K) : density, (SI units: kg/m3)
: density, (SI units: kg/m3)